Frequently asked questions about activity flow mapping (Cole et al., 2016; Nature Neuroscience)

We recently published a paper in Nature Neuroscience that we’re quite excited about. It’s titled “Activity flow over resting-state networks shapes cognitive task activations“. Here we are going to go over some lesser-known aspects of the study. We will begin, however, with a basic overview of the results.

Briefly, we sought to gain some clarity on what the cognitive relevance of resting-state networks might be. These networks have been studied extensively with hundreds of papers now being published each year using resting-state fMRI. But what do they have to do with cognition? In particular, how do resting-state networks mechanistically relate to cognitive functions?

We hypothesized that activity flow – the movement of activation amplitudes between brain regions – is the network mechanism that explains the relevance of resting-state networks to cognitive activations (and therefore to cognition). We found strong support for this hypothesis using both a simple computational model and empirical fMRI data.

I’ll now switch to a frequently asked questions (FAQ) format, digging into some lesser-known conclusions from the study:

Wasn’t this already known based on previous studies showing that resting-state networks are similar to a variety of task-evoked activation patterns?

Those studies certainly suggested there is some relationship between resting-state networks and cognition. Yet it has remained unclear what that relationship might be. It has been especially unclear what knowing something about a resting-state network (such as an alteration in a patient group) tells us about cognitive functionality. In other words, what does resting-state network organization tell us mechanistically about cognitive activations?

We already know the mechanism that relates activations and connectivity: resting-state networks reflect the history of activation patterns across tasks. What does this activity flow hypothesis add?

Yes, one prominent theory has been that resting-state networks reflect the history of activation patterns across many tasks. This would involve Hebbian-like learning, in which repeated coactivations would lead to higher resting-state functional connectivity (activations→connectivity). There is some evidence for this, yet we thought there was a much simpler explanation: Rather than activations primarily influencing connectivity, resting-state functional connectivity likely primarily influences activations.

Logically, the connectivity→activations scenario is actually necessary for the activations→connectivity scenario to be functionally effective. To illustrate this, imagine that activations slowly shape connectivity patterns. What, mechanistically, would this do for cognitive computations? It is not clear, unless connectivity changes immediately begin impacting activations. This would allow the connectivity changes to begin altering cognitive computations. Thus, even under the activations→connectivity scenario there is an important role for a more prominent (given its faster time scale and more direct causal relationship) connectivity→activations mechanism.

So you hypothesized that resting-state functional connectivity shapes cognitive task activations. But is this even plausible, given that one is measured during rest and the other during task performance?

Yes. We recently found that resting-state networks are present across a wide variety of task performance contexts. This shows that resting-state functional connectivity can plausibly describe the routes of activity flow even during tasks.

In the present study we began by using a simple computational model to show this plausibility even more clearly. The model was as abstract as possible to facilitate generalization of the results – it simply involved units (representing brain regions) interacting via a standard “rate code”. A particular network organization was imposed using structural connectivity and aggregate synaptic connectivity strengths. We then simulated fMRI data collection to ensure that our inferences would generalize to fMRI data as well.

We found that resting-state functional connectivity emerged with no additional mechanistic features added to the model. And the observed functional connectivity matched the synaptic connectivity pattern (which built on the structural connectivity pattern) quite well.

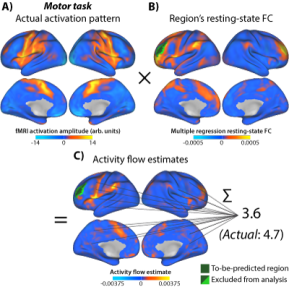
Further, we found that task-evoked activations in a held-out location could be predicted based on estimated activity flow through the observed resting-state networks. This demonstrated the plausibility of activity flow linking resting-state functional connectivity with cognitive task activations.

This activity flow mapping approach isn’t real activity flow, which involves propagation of activity that has a direction and a temporal lag. Why do you call it “activity flow” when it does not have directionality or a temporal lag?

This was a major reason we included a computational model with real activity flow (i.e., with temporal lags and directionality) in the study. We knew the ground truth activity flow (since we defined the network organization in the model), and so we could see if the activity flow mapping procedure was an accurate estimate of real activity flow. It was, though it did not indicate directionality. We plan to extend activity flow mapping to include directionality in the future. But in the meantime we found strong evidence that activity flow mapping-based estimates reflect real activity flow (and this was true even after fMRI simulation in the model).

I would not necessarily agree that the distinction between brain activations and brain connectivity corresponds to the distinction between localized versus distributed processing. Many folks look at brain activations in terms of distributed processing.

I agree that the activation vs. connectivity perspectives do not map directly onto the localized vs. distributed distinction. Rather, we were trying to focus on the subset of activation-based researchers who think of what they do as studying primarily localized processing. This was quantified in the computational model in Figure 1B, with an explicit manipulation of localized vs. distributed processing. It was shown that if the network was primarily performing localized processing (i.e., having high within-region connectivity such that each region was largely isolated from other regions) then activity flow mapping won’t work. Given that it did work in the real brain therefore shows that the brain’s computations are quite distributed in nature.

It seems important to understand what the multiple-regression functional connectivity approach involved, since it performed so much better than Pearson correlations for activity flow mapping. Is the multiple regression approach akin to partial correlation-based functional connectivity?  If so, why not describe it that way?

It is actually different than partial correlation, though very related. It’s actually akin to a semipartial correlation, since the other regions’ time series are not regressed out of the to-be-predicted time series. (All regions’ time series are regressed out of all other regions’ time series for partial correlation). Also, unlike partial correlation the resulting statistic (here, the beta value) is in the raw units of the to-be-predicted region. This allows us to predict the held-out region’s activation level in the actual units of that region (based on resting-state fMRI data).

I think I am not fully appreciating how the computational model does or does not constrain any interpretations of the empirical data. How could the computational modeling have come out differently that would have changed your interpretation of the empirical data?

Here’s what the computational model adds:

1. The model implements “ground truth” real activity flow (with temporal features and directionality), and shows that activity flow mapping properly reflects that real activity flow despite not fully reflecting the temporal aspects. In other words, it validates activity flow mapping as a method.
2. The model shows that activity flow mapping works despite the hemodynamic response and downsampling from fMRI. (The real activity flow was implemented in the model prior to fMRI simulation).
3. Most relevant for your question: The model simulates what it would be like if the brain primarily involved localized processing. It is found that if localized processing is very high then activity flow mapping will not work. (Localized processing is quantified as recurrent connectivity, with each brain region influencing itself more on the subsequent time point the higher the localized processing parameter is.) This makes the empirical demonstration of activity flow mapping a non-trivial result, since it did not have to come out that way. Further, this makes it such that the empirical result rules out the possibility that brain processing is highly localized, with individual brain regions massively altering their inputs without faithfully sending all (or most) of those alterations out to other regions.

I hope this FAQ was interesting, or at least informative. I might post more questions or other details about activity flow mapping in future posts. Please add comments here with more questions!

–MWCole